Absorption of Gamma Rays in Lead

Brief

The brief is as follows.

Find what effect varying the width of a lead block has on the transmission of gamma rays through the said block.

Method

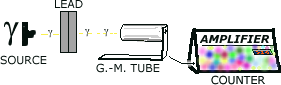
Source. Piece of lead if thickness x. G.M.-Tube. Amplifier and Counter. That basically describes the setup.

We will use several pieces of lead to get several count rates for several values of x.

Prediction

Based on idea that the fewer MeV of gamma, the harder it will be for it penetrate further.

Results

Raw and Average Data

x /[mm]	Count Rate	Time /[s]	Average A/[s-1]
background	57	120	0.475
0.00	114	60
0.00	137 *	60
0.00	122 *	60
0.00	115	60	2.03
23.25	57 *	60
23.25	48 *	60	0.875 *
12.18	81 *	60
12.18	54 *	60	1.13
6.44	89	60
6.44	89	60	0.98
1.13	100	60
1.13	108	60	1.73

Errors, Limitations, Improvements, Mistakes, Changes

Errors were quite large.

We were limited by time.

An important improvement would have been to turn the G.M.-Tube so that it was not facing the source. This is because by going through the plastic coating, the energy of each gamma photon would have been reduced and therefore would be more ready to ionise the Argon, thus giving us a more correct figure. However since this error was constant, we can actually ignore it! Wow...

The data's error limits have not been calculated exactly, but can be aproximated if it is assumed error in timing to be ±1s, count rate ±10 or more (examine the raw results) giving a percentage error in the region of 20%. It would be difficult to tell exactly without further research.

Although I was adamant that we make many readings, my colleagues did not wish to even do two tests (I did it without their knowledge since I had placed myself in the useful and enviable position of "guy in charge of the counter"). Had we done a more thourough piece of work, the data error would be much reduced (notably those results marked with an asterisk *).

The data ignores absorbtion by air.

We made no other mistakes.

Analysis

The actual graph is more of a inverse square law, actually it's not, it's an exponential fall.

I = I₀e^-kx

Or, more conventially,

I = I₀e^-mx

Where I = Intensity (basically count rate), I₀ = Intensity at x = 0 and k or m are some sort of useful constant.

Conclusion

g-rays have therefore no definite range in lead (or, by extension, any medium). Postexperimental research indicates that to reduce intensity to a tenth of it's original intensity (I₀), one needs 30mm and 40mm for 1MeV and 10MeV g-rays respectively.

And such is the extent of my work.