Using Data Mining Techniques with the 2df QSO Redshift Survey Spectra to Locate Damped Lyman Alpha Systems

Ian Hickson

Abstract

Spectra from the 2df QSO redshift survey are analysed first using algorithmic methods and then using a neural network. The data is found to be too unpredictable for simple algorithms to detect DLAs, although many oddities are discovered and the algorithms could be used for looking for other, more obvious patterns. This conclusion is backed by the neural network results, which indicate that the data is too varied for a simple back-propagation error correction algorithm. It is suggested that to avoid falling into local minima, a neural network could be evolved using genetic algorithm techniques. A C++ implementation of a feed forward trilayer perceptron is provided.

1. Introduction

The aim of this project was to use automated techniques to locate previously undiscovered damped Lyman alpha systems amongst the 2df QSO Redshift Survey data. [1]

1.1. Damped Lyman alpha systems

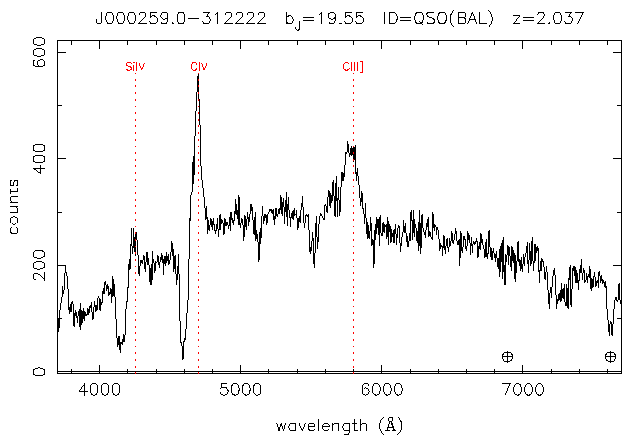
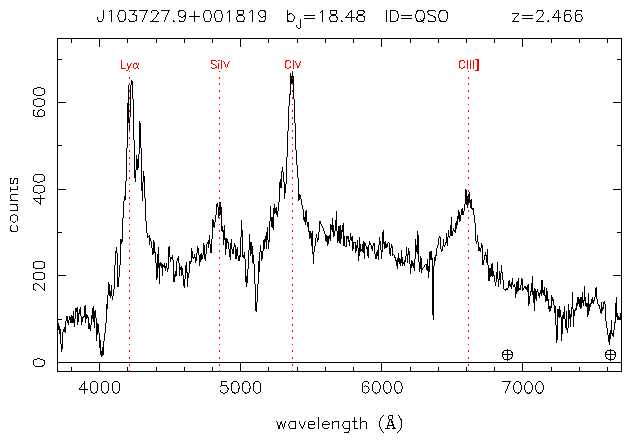
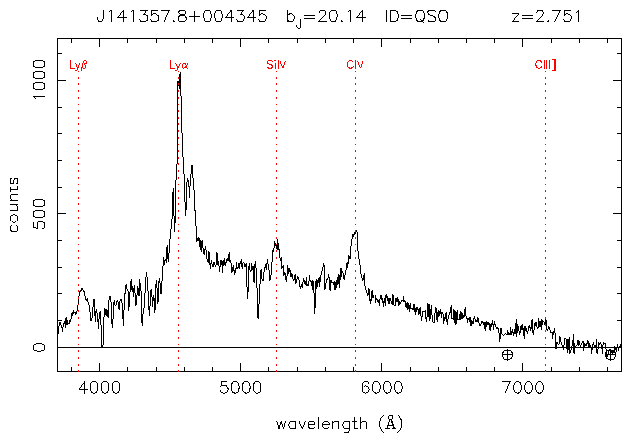
Damped Lyman alpha systems arise when light emitted from a quasistellar object (or QSO) goes through a gas cloud on its way to the observer. [2] When the photons interact with the hydrogen atoms in the gas cloud, the hydrogen atoms absorb some of the radiation, primarily the photons with wavelength 1216Å, the Lyman series of the Hydrogen atom.

Due to the doppler shift caused by cosmic expansion, the photons in question usually correspond to different inital wavelengths and show up as dips at different wavelengths upon reaching the observer. The redshift can be used to determine the distance to the gas cloud, and the width of the damped system can be used to determine the column depth of the cloud.

It is believed that gas clouds dense enough to noticably affect backlighting QSO spectra are galaxies in early stages of formation. As data on protogalaxies and gas clouds is useful in refining models for galactic evolution, damped Lyman alpha systems found in the data highlight targets for further study.

Below are some typical damped Lyman alpha systems. (All graphs courtesey of the 2df QSO 10K Catalogue. [1])

J000259.0-312222a

This spectrum is damped between 4100Å and 4200Å. This is a very narrow dip and represents the smallest such feature that should be considered a match.

J103727.9+001819

A spectrum with a narrow dip around 4000Å

J141357.8+004345

This spectrum shows a classic Lyman forest at around 4000Å, and was highlighted by P. J. Outram, et al [3] as a subject for further study.

1.2. The 2df QSO redshift survey

The survey was conducted using one of the world's most advanced telescope systems, the Anglo-Australian Telescope 2 Degree Field facility.

The Anglo-Australian Telescope (AAT), completed in June 1975 [4], is an equatorially mounted 4-metre telescope. Prior to the 1970s, most of the large telescopes were located in the northern hemisphere, and were thus unable to study many of the closest radio galaxies, as well as the center of our own. [5]

The AAT can be used in many different configurations, using various instruments and detectors. In the configuration used for the 2df QSO redshift survey, the AAT consisted of a wide field corrector, an atmospheric dispersion compensator, a robot gantry, two spectrographs, and a tumbling mechanism. In this configuration the covers wavelengths from 3500Å to 8000Å.

The tumbling mechanism enabled one field plate of optic fibres to be configured by the robot while simultaneously another plate of optic fibres, connected to the spectrographs, was analysed. As both these processes take approximately an hour to complete, this setup allowed the spectra to be collected simultaneously and continuously in an automated fashion. [6] Each spectrograph was able to analyse 200 objects at a time, allowing for a total of 400 spectra to be collected during each cycle.

1.3. The 2QZ 10K Catalogue

Note that the survey was conducted for the purpose of confirming the identity of suspected QSOs and to find their redshift. For this reason, the typical signal-to-noise ratio (S/N) of the spectra is in the region of 10, and the resolution appoximately 8Å. This is not optimal for searching for DLAs. [3]

2. The algorithmic approach

The first approach consisted of a set of algorithms applied to the data, in a traditional deterministic manner.

2.1. Basic program design

The program evolved significantly over the life of this project, but the main design remained the same throughout.

First, data is extracted from the FITS (Flexible Image Transport System) data files provided on the 2df data CDROM. [1] To extract data from the FITS files, the CFITSIO library was used. [7] This library provides a portable subroutine-based API for reading and writing FITS data files.

The FITS files used by 2df survey consisted of a 1024 element spectrum (scaled by the standard BSCALE and BZERO headers), a 1024 boolean bad pixel mask, and a median sky spectrum. [8] [9]

Originally, spectra not associated with QSOs were then discarded. However, it was discovered that the spectrum labelling of the 2df data is unreliable, and this step was sebsequently skipped.

Finally, the data was smoothed and then analysed, flagging potential matches.

Some implementation details, such as optimisations used to ease development, shall not be described in this report.

2.2. Smoothing

The spectra have a lot of high frequency noise. To reduce the number of false negatives, the data had to be smoothed.

2.2.1. Bad pixels

The data included, for each spectrum, a bad pixel mask. This is a list of which of the 1024 values should be considered invalid during analysis.

Bad pixels can arise from several different sources, including poor weather, and edge effects (all the spectra have some number of bad pixels at the start and end of the data).

2.2.2. Moving average

The simplest smoothing algorithm used consisted simply of applying a smoothing average: taking the mean of the valid values present in the last n points as the value of each pixel.

Various windows were tried, a window of 10 data points resulted in reasonable smoothing without losing the major features of the data.

Because of the bad pixels, there were points in the output of this algorithm that would have no value (if more than n bad pixels appeared together). To work around this, a simple linear extrapolation was then applied to the gaps.

While this algorithm had a moderate success in removing some of the noise, it was not satisfactory and was quickly discarded.

2.2.3. Fourier transformation

This second method provided much smoother results. A fourier transform was used to perform a transformation into the frequency domain, cut out the high frequency noise, then convert the data back to the time domain. (Note that technically the time domain was the frequency domain and the frequency domain the time domain, but this is ignored here for clarity.)

The transform was implemented using the FFTW, a high performance portable API that uses self-adapting techniques to optimise itself for the machine architecture and type of data being transformed. [10]

Trial and error found that cutting approximately the top 90% of the data resulted in the smoothest data still resembling the original.

For more detail on the FFTW algorithms used, see [11].

2.3. Patterns: Extended Minima

The initial approach was developed prior to having analysed the data in much detail. It was based on the assumption that damped systems would characteristically approach zero, while undamped signals would not.

2.3.1. Algorithm

For each spectrum, each good pixel was examined in turn. A count of how many pixels in a row had a value less than a particular threshold was found. Any spectrum with a suitably wide number series of such low values was then flagged.

The threshold used was a little above 0, as the intention was to catch damped systems that approached the zero baseline.

2.3.2. Conclusions

Unfortunately, it turns out that a large number of the spectra are miscalibrated, resulting in most having numbers near, or even below, zero. (Note that the spectra have indeed not been flux calibrated, so this is not unusual.) Therefore this technique is unsuitable for finding damped systems in the 2QZ 10k catalogue.

2.3.3. Discoveries

While no damped Lyman alpha systems were discovered using this technique, several oddities were flagged.

J024412.2-293014

This spectrum appears to be galactic in nature (rather than a QSO, as it is labelled).

J215555.2-283710a

This spectrum has a mean value less than zero, indicating significant miscalibration.

2.4. Patterns: Gradients

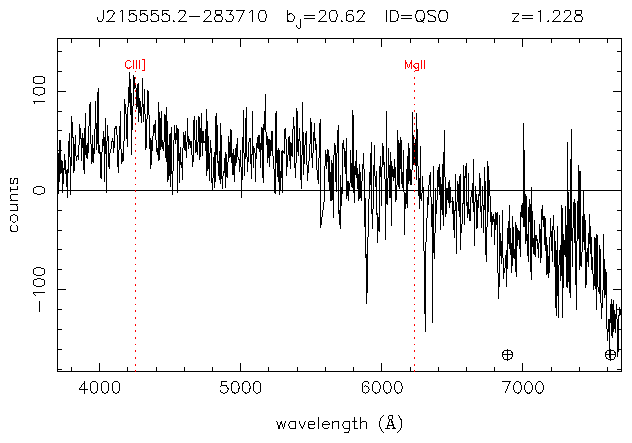
This approach was built on the experience gained from examining the spectra highlighted by the zeroes algorithm.

It is based on searching for a period of characteristic decrease in value over a short period, following a similar characteristic increase in value.

2.4.1. Algorithm

For each value in the array, compare the value to the previous one. If the last few values have been decreasing but the last step is an increase, remember this point as the last decrease and remember how many decreases happened in a row. Otherwise, if this is an increase and there have been enough increases in a row, and the last decrease is suitably far away, and there were enough decreases in a row, flag this spectrum and move to the next one.

2.4.2. Conclusions

In practice, this does not work at all, because the signal (even after excessive smoothing) still contains perturbations (high frequency noise) on the up and down curves.

Another problem is that this algorithm highlighted many spectra with two adjacent clean peaks.

2.5. Looking for dips: Version 2

To get around the limitations of the first version, a new algorithm was developed by looking for the following characteristics:

• The dips have a minimum width and a maximum width.
• The average value in a dip is lower than the average values on either side of the dip.
• The sides of the dip have to change by a certain amount within a certain width.

The algorithm is more involved and is best explained through the following pseudo-code:

1. Set lastDown and lastUp to 0.
2. Starting at a certain distance from the left margin (to skip edge noise and have enough room to later average it if required), and stepping through each value until a certain distance from the end of the data:
   1. If the value of the pixel a certain distance to the left divided by the value of the pixel at the current location is greater than a threshold drop fraction,
      1. Store the position of the pixel in lastDown.
   2. If the value of the pixel a certain distance to the right divided by the value of the pixel at the current location is greater than a threshold drop fraction,
      1. Store the position of the pixel in lastUp.
   3. If lastDown is not 0, and lastUp - lastDown is within the range of minimum and maximum widths for a dip,
      1. Find the mean value between the lastDown and lastUp positions.
      2. Find the mean value for a certain distance before lastDown.
      3. Find the mean value for a certain distance after lastUp.
      4. Check that the first mean is lower than the other two means by a certain amount. If it is, flag this spectrum and move on to the next one.

2.5.1. Discoveries

Three spectra were identified as potential forming galaxies, the first two may actually be galaxies in the foreground, and the third may potentially be a backlit DLA.

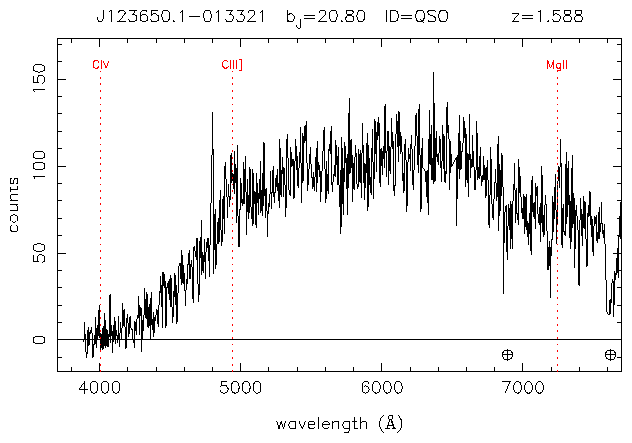
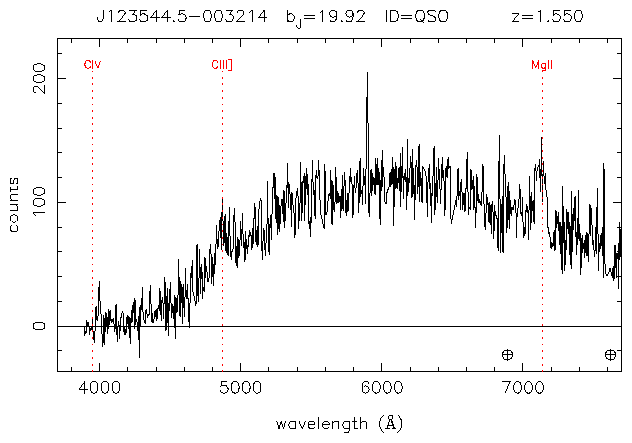
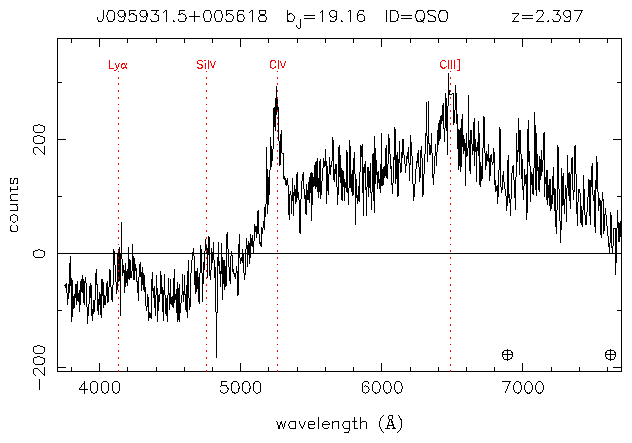
The following spectra were also flagged. (Note that the data points are in the 0..1023 range of the data file, not in angstroms.)

• J012122.9-312825a may have a dip between data points 372 and 585.
• J024504.5-292103a may have a dip between data points 365 and 507.
• J110735.9-023414a may have a dip between data points 579 and 763.
• J113701.4-001940b may have a dip between data points 486 and 616.
• J124557.8+001757a may have a dip between data points 519 and 648.
• J124604.8+002714a may have a dip between data points 594 and 732.
• J131759.1+014012a may have a dip between data points 656 and 816.
• J134453.0-010637a may have a dip between data points 605 and 731.
• J143613.1-003657a may have a dip between data points 209 and 384.
• J215638.8-274941a may have a dip between data points 576 and 789.
• J222601.6-300959a may have a dip between data points 512 and 803.
• J224550.9-301903a may have a dip between data points 486 and 615.
• J230624.7-280338b may have a dip between data points 350 and 605.
• J235414.5-300225a may have a dip between data points 650 and 792.

2.5.2. Conclusions

In practice, this fails to take into the effects of fluctuations in the data. Even when ignoring a lot of high frequency noise (see the section on smoothing by fourier transform), this technique would still catch two high spikes around a low spike. The flagged spectra did not really fit the DLA profile.

2.6. Directions for future researh

These algorithms could be improved in two main ways. Firstly, instead of looking at mean values in the last algorithm, median values could be examined. This would reduce the sensitivity to peak noise.

A second possible approach is to analyse the data in the frequency domain (technically the time domain, since the original data is a function of frequency) instead of examining the data after smoothing. This option was largely ignored during this analysis but could potentially lead to greater resilience against fluctuations.

3. The neural network approach

Neural networks are loosely based on what is believed to be the structure of human brains. Human brains are formed from large networks of neurons, cells that consist of many 'input' dendrites and many 'output' dendrites. Dendrites are interconnected by synapses, whose chemical state affects the weight with with the signal will impact the following neuron.

To train the brain, it is believed that different responses trigger different chemicals to bathe the synapses, changing the relative impact of each dendrite on the next cell.

In a real human brain there are roughly 10¹⁰ neurons each with up to several thousand synapses contained on the dendrites, giving up to a maximum of 10¹⁴ synapses [12].

Neural networks are similarly formed. The particular network type used in this investigation is known as a feed forward trilayer perceptron, using a back-propagating differential error correction algorithm for training.

3.1. Feed Forward Trilayer Perceptrons (FFTPs)

FFTPs are Feed Forward Multilayer Pereptrons (FFMPs) with two hidden layers. The implementation used here is based on the FFMP implementation discussed by Bailer-Jones, et al. [12]

FFMPs are simple mathematical models of the biological neural networks described above. Neurons are replaced by transfer functions, dendrites are replaced by arrays, synapses by weights, and training chemicals by differentiation.

Instead of a large network of cells all interconnected, a well defined number of layers is selected, and every combination of weights from the input layer to the first layer, the first layer to the second layer, and so on up to the output layer is then given a weight.

In addition to connections between every value of each layer to the next, an additional (arbitrary) value is connected to each value of each layer. These bias nodes are required to offset values. For example even if all the imputs are zero, the bias node allows the first layer to use non-zero values as arguments to the transfer function, allowoing the full range of output. Without bias nodes the only argument possible would be zero.

3.1.1. Transfer Function

The transfer function used is that recommended by Bailer-Jones, et al, namely the hyperbolic tangent.

This function has the property that all real inputs give an output in the range of -1..1. However, it also introduces the possibility for network saturation, where the weights grow such that every node in a layer has the value 1 (or -1) and the data therefore has no relation to the input. This must be avoided by not over-training the network and by using small inital weights.

3.1.2. Equations

The notation used here is based on that used by Bailer-Jones, et al.

$x_i$

The input data. The i subscript's range is 1..I+1, where I is the index of the last input node, so the I+1th node is the first hidden layer's bias node.

$p_j$

The first hidden layer. The j subscript's range is 1..J+1, where J is the index of the last node in the first hidden layer to be affected by the input layer, and the J+1th node is the second hidden layer's bias node.

$q_k$

The second hidden layer. The k subscript's range is 1..K+1, where K is the index of the last node in the second hidden layer to be affected by the first hidden layer, and the K+1th node is the output layer's bias node.

$y_l$

The output layer. The y subscript's range is 1..L, where L is the index of the last node in the output layer.

$w_{i,j}$

The weights between the $x_{i..I+1}$ and $p_{j..J}$ layers.

$w_{j,k}$

The weights between the $p_{j..J+1}$ and $q_{k..K}$ layers.

$w_{k,l}$

The weights between the $q_{k..K+1}$ and $y_{l..L}$ layers.

The input layer is given by:

$x_i=\{\begin{array}{cc}1& i=I+1\\ \mathrm{input}\left(i\right)& \text{otherwise}\end{array}$

Each node in the first hidden layer is then calulated by summing each input (including the bias node) multiplied by a weighting value, and finding the hyperbolic tangent of the result:

$p_j=\{\begin{array}{cc}1& j=J+1\\ \tanh \left(\sum _{i^{\prime }}^I{w}_{i^{\prime },j}{x}_{i^{\prime }}+w_{I+1,j}\right)& \text{otherwise}\end{array}$

$q_k=\{\begin{array}{cc}1& k=K+1\\ \tanh \left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k}{p}_{j^{\prime }}+w_{J+1,k}\right)& \text{otherwise}\end{array}$

$y_l=\sum _{k^{\prime }}^K{w}_{k^{\prime },l}{q}_{k^{\prime }}+w_{K+1,l}$

3.2. Back-Propagating Differential Error Correction

The training consists of supervised learning by minimization of an error function with respect to all of the network weights. [12] The error function used here is the sum-of-squares error:

$e=\frac{1}{2}\sum _{l^{\prime }}^L{\beta }_{l^{\prime }}{\left(y_{l^{\prime }}-T_{l^{\prime }}\right)}^2$

This represents the total difference between the actual output and the ideal output. By minimising this number we move towards a more ideal output, and by finding how much a small change in each weight would affect the error function, we can estimate how much change in the weights is required to move towards the minimum.

For the last set of weights, differentiating equation 5 with respect to the weights gives:

$\frac{\partial e}{\partial w_{k,l}}=\frac{1}{2}\sum _{l^{\prime }}^L{\beta }_{l^{\prime }}2\left(y_{l^{\prime }}-T_{l^{\prime }}\right)\frac{\partial y_l}{\partial w_{k,l^{\prime }}}$

...where:

$\frac{\partial y_{l^{\prime }}}{\partial w_{k,l}}=\sum _{k^{\prime }}^K{\delta }_{k^{\prime }k}{\delta }_{l^{\prime }l}{q}_{k^{\prime }}+{\delta }_{K+1k}{\delta }_{l^{\prime }l}$

...and $\delta$ is the Kronecker delta function.

This simplifies to:

$\frac{\partial y_{l^{\prime }}}{\partial w_{k,l}}=\{\begin{array}{cc}{\delta }_{l^{\prime }l}& k=K+1\\ {\delta }_{l^{\prime }l}{q}_k& \text{otherwise}\end{array}$

Substituting 8 into 6:

$\frac{\partial e}{\partial w_{k,l}}=\{\begin{array}{cc}\frac{1}{2}\sum _{l^{\prime }}^L{\beta }_{l^{\prime }}2\left(y_{l^{\prime }}-T_{l^{\prime }}\right){\delta }_{l^{\prime }l}& k=K+1\\ \frac{1}{2}\sum _{l^{\prime }}^L{\beta }_{l^{\prime }}2\left(y_{l^{\prime }}-T_{l^{\prime }}\right){\delta }_{l^{\prime }l}{q}_k& \text{otherwise}\end{array}$

...this simplifies to:

$\frac{\partial e}{\partial w_{k,l}}=\{\begin{array}{cc}{\beta }_l\left(y_l-T_l\right)& k=K+1\\ {\beta }_l\left(y_l-T_l\right)q_k& \text{otherwise}\end{array}$

For the middle set of weights,

$\frac{\partial e}{\partial w_{j,k}}=\frac{1}{2}\sum _{l^{\prime }}^L{\beta }_{l^{\prime }}2\left(y_{l^{\prime }}-T_{l^{\prime }}\right)\frac{\partial y_{l^{\prime }}}{\partial w_{j,k}}$

...where:

$\frac{\partial y_{l^{\prime }}}{\partial w_{j,k}}=\sum _{k^{\prime }}^K{w}_{k^{\prime },l^{\prime }}\frac{\partial q_{k^{\prime }}}{\partial w_{j,k}}$

$\frac{\partial q_{k^{\prime }}}{\partial w_{j,k}}=\{\begin{array}{cc}0& k^{\prime }=K+1\\ {\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right)\left(\sum _{j^{\prime }}^J{\delta }_{j^{\prime }j}{\delta }_{k^{\prime }k}{p}_{j^{\prime }}+{\delta }_{J+1j}{\delta }_{k^{\prime }k}\right)& \text{otherwise}\end{array}$

Simplifying:

$\frac{\partial q_{k^{\prime }}}{\partial w_{j,k}}=\{\begin{array}{cc}0& k^{\prime }=K+1\\ {\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right){\delta }_{k^{\prime }k}& j=J+1\\ {\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right){\delta }_{k^{\prime }k}{p}_j& \text{otherwise}\end{array}$

Substituting 14 into 12, and noting the sum over $k^{\prime }$ does not exceed K:

$\frac{\partial y_{l^{\prime }}}{\partial w_{j,k}}=\{\begin{array}{cc}\sum _{k^{\prime }}^K{w}_{k^{\prime },l^{\prime }}{\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right){\delta }_{k^{\prime }k}& j=J+1\\ \sum _{k^{\prime }}^K{w}_{k^{\prime },l^{\prime }}{\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right){\delta }_{k^{\prime }k}{p}_j& \text{otherwise}\end{array}$

Simplifying:

$\frac{\partial y_{l^{\prime }}}{\partial w_{j,k}}=\{\begin{array}{cc}{w}_{k,l^{\prime }}{\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k}{p}_{j^{\prime }}+w_{J+1,k}\right)& j=J+1\\ w_{k,l^{\prime }}{\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k}{p}_{j^{\prime }}+w_{J+1,k}\right)p_j& \text{otherwise}\end{array}$

Substituting 16 into 11 and cancelling the twos:

$\frac{\partial e}{\partial w_{j,k}}=\{\begin{array}{cc}\sum _{l^{\prime }}^L{\beta }_{l^{\prime }}\left(y_{l^{\prime }}-T_{l^{\prime }}\right)w_{k,l^{\prime }}{\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k}{p}_{j^{\prime }}+w_{J+1,k}\right)& j=J+1\\ \sum _{l^{\prime }}^L{\beta }_{l^{\prime }}\left(y_{l^{\prime }}-T_{l^{\prime }}\right)w_{k,l^{\prime }}{\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k}{p}_{j^{\prime }}+w_{J+1,k}\right)p_j& \text{otherwise}\end{array}$

Finally for the first set of weights,

$\frac{\partial e}{\partial w_{i,j}}=\frac{1}{2}\sum _{l^{\prime }}^L{\beta }_{l^{\prime }}2\left(y_{l^{\prime }}-T_{l^{\prime }}\right)\frac{\partial y_{l^{\prime }}}{\partial w_{i,j}}$

...where:

$\frac{\partial y_{l^{\prime }}}{\partial w_{i,j}}=\sum _{k^{\prime }}^K{w}_{k^{\prime },l^{\prime }}\frac{\partial q_{k^{\prime }}}{\partial w_{i,j}}$

$\frac{\partial q_{k^{\prime }}}{\partial w_{i,j}}=\{\begin{array}{cc}0& k^{\prime }=K+1\\ {\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right)\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}\frac{\partial p_{j^{\prime }}}{\partial w_{i,j}}& \text{otherwise}\end{array}$

$\frac{\partial p_{j^{\prime }}}{\partial w_{i,j}}=\{\begin{array}{cc}0& j^{\prime }=J+1\\ {\mathrm{sech}}^2\left(\sum _{i^{\prime }}^I{w}_{i^{\prime },j^{\prime }}{x}_{i^{\prime }}+w_{I+1,j^{\prime }}\right)\left(\sum _{i^{\prime }}^I{\delta }_{i^{\prime }i}{\delta }_{j^{\prime }j}{x}_{i^{\prime }}+{\delta }_{I+1i}{\delta }_{j^{\prime }j}\right)& \text{otherwise}\end{array}$

Simplifying:

$\frac{\partial p_{j^{\prime }}}{\partial w_{i,j}}=\{\begin{array}{cc}0& j^{\prime }=J+1\\ {\mathrm{sech}}^2\left(\sum _{i^{\prime }}^I{w}_{i^{\prime },j^{\prime }}{x}_{i^{\prime }}+w_{I+1,j^{\prime }}\right){\delta }_{j^{\prime }j}& \text{<mi>i</mi> <mo>=</mo> <mi>I</mi> <mo>+</mo> <mn>1</mn>}\\ {\mathrm{sech}}^2\left(\sum _{i^{\prime }}^I{w}_{i^{\prime },j^{\prime }}{x}_{i^{\prime }}+w_{I+1,j^{\prime }}\right){\delta }_{j^{\prime }j}{x}_i& \text{otherwise}\end{array}$

Substituting 22 into 20 and noting $j^{\prime }$ never reaches J+1:

$\frac{\partial p_{j^{\prime }}}{\partial w_{i,j}}=\{\begin{array}{cc}0& k^{\prime }=K+1\\ {\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right)\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{\mathrm{sech}}^2\left(\sum _{i^{\prime }}^I{w}_{i^{\prime },j^{\prime }}{x}_{i^{\prime }}+w_{I+1,j^{\prime }}\right){\delta }_{j^{\prime }j}& \text{<mi>i</mi> <mo>=</mo> <mi>I</mi> <mo>+</mo> <mn>1</mn>}\\ {\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right)\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{\mathrm{sech}}^2\left(\sum _{i^{\prime }}^I{w}_{i^{\prime },j^{\prime }}{x}_{i^{\prime }}+w_{I+1,j^{\prime }}\right){\delta }_{j^{\prime }j}{x}_i& \text{otherwise}\end{array}$

Simplifying:

$\frac{\partial p_{j^{\prime }}}{\partial w_{i,j}}=\{\begin{array}{cc}0& k^{\prime }=K+1\\ {\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right)w_{j,k^{\prime }}{\mathrm{sech}}^2\left(\sum _{i^{\prime }}^I{w}_{i^{\prime },j}{x}_{i^{\prime }}+w_{I+1,j}\right)& \text{<mi>i</mi> <mo>=</mo> <mi>I</mi> <mo>+</mo> <mn>1</mn>}\\ {\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right)w_{j,k^{\prime }}{\mathrm{sech}}^2\left(\sum _{i^{\prime }}^I{w}_{i^{\prime },j}{x}_{i^{\prime }}+w_{I+1,j}\right)x_i& \text{otherwise}\end{array}$

Substituting 24 into 19 and noting $k^{\prime }$ never reaches K+1:

$\frac{\partial y_{l^{\prime }}}{\partial w_{i,j}}=\{\begin{array}{cc}\sum _{k^{\prime }}^K{w}_{k^{\prime },l^{\prime }}{\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right)w_{j,k^{\prime }}{\mathrm{sech}}^2\left(\sum _{i^{\prime }}^I{w}_{i^{\prime },j}{x}_{i^{\prime }}+w_{I+1,j}\right)& \text{<mi>i</mi> <mo>=</mo> <mi>I</mi> <mo>+</mo> <mn>1</mn>}\\ \sum _{k^{\prime }}^K{w}_{k^{\prime },l^{\prime }}{\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right)w_{j,k^{\prime }}{\mathrm{sech}}^2\left(\sum _{i^{\prime }}^I{w}_{i^{\prime },j}{x}_{i^{\prime }}+w_{I+1,j}\right)x_i& \text{otherwise}\end{array}$

Substituting 25 into 18 and cancelling the twos:

$\frac{\partial e}{\partial w_{i,j}}=\{\begin{array}{cc}\sum _{l^{\prime }}^L{\beta }_{l^{\prime }}\left(y_{l^{\prime }}-T_{l^{\prime }}\right)\sum _{k^{\prime }}^K{w}_{k^{\prime },l^{\prime }}{\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right)w_{j,k^{\prime }}{\mathrm{sech}}^2\left(\sum _{i^{\prime }}^I{w}_{i^{\prime },j}{x}_{i^{\prime }}+w_{I+1,j}\right)& \text{<mi>i</mi> <mo>=</mo> <mi>I</mi> <mo>+</mo> <mn>1</mn>}\\ \sum _{l^{\prime }}^L{\beta }_{l^{\prime }}\left(y_{l^{\prime }}-T_{l^{\prime }}\right)\sum _{k^{\prime }}^K{w}_{k^{\prime },l^{\prime }}{\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right)w_{j,k^{\prime }}{\mathrm{sech}}^2\left(\sum _{i^{\prime }}^I{w}_{i^{\prime },j}{x}_{i^{\prime }}+w_{I+1,j}\right)x_i& \text{otherwise}\end{array}$

The implementation of these equations (26, 18 and 10) can be optimised by noting that some of the terms (for example the first sech term in equation 26) are common to all of the input values and can therefore be precalculated. This reduces the total instruction count significantly.

3.3. Implementation

The implementation of the Feed Forward Trilayer Pereptron was written in C++. A class (FeedForwardTrilayerPerceptron, declared in fftw.h and defined in fftw.cpp, see appendix 7) represents a single trainable neural network, with the following methods:

FeedForwardTrilayerPerceptron(int, int, int, int, double)

A constructor that creates a randomly initialised perceptron of the specified size. The first four arguments represent the sizes of the input layer, two hidden layers, and output layer respectively (not including hidden nodes). The last argument is a floating point number representing the maximum absolute value to use for the weights. (For instance if it is 0.05 then the random weights will be in the range -0.05..0.05.)

FeedForwardTrilayerPerceptron(int, int, int, int, std::vector<double>*)

A constructor that creates a perceptron of the specified size initialised from specified weights. The first four arguments represent the sizes of the input layer, two hidden layers, and output layer respectively (not including hidden nodes), and the last argument is a pointer to a standard template library (STL) vector containing the weights required (including those required for hidden nodes). The vector returned by GetCharacteristics() is in this format.

FeedForwardTrilayerPerceptron(istream&)

A constructor that creates a perceptron based on parameters stored on an STL stream in the format created by Save().

~FeedForwardTrilayerPerceptron()

The destructor.

std::vector<double>* Run(std::vector<double>*)

Takes a pointer to a vector containing the input data and returns a pointer to a new vector containing the outputs. The caller is responsible for destroying the new vector.

The outputs are generated from the inputs by using the algorithm given in section 3.1.2, with input(1..I) given by the the vector passed as an argument, and the output given by y.

std::vector<double>* Test(std::vector<double>*, std::vector<double>*, std::vector<double>&)

This is the heart of the training algorithm.The arguments are the input, the ideal output (T), and the importance to be attached to each output ($\beta$). The result is a pointer to a new vector containing the value of e with respect to each individual weight in the network. The caller is responsible for destroying the new vector.

The order of the values in the vector returned is internal to the FeedForwardTrilayerPerceptron implementation, as it is dependent on the exact implementation of the training algorithm. Therefore, nothing should be assumed about the order of the values in this array.

The values of $\frac{\partial e}{\partial w_{i,j}}$ are obtained from the equations derived in section 3.2, namely:

$\frac{\partial e}{\partial w}=\{\begin{array}{cc}\sum _{l^{\prime }}^L{\beta }_{l^{\prime }}\left(y_{l^{\prime }}-T_{l^{\prime }}\right)\sum _{k^{\prime }}^K{w}_{k^{\prime },l^{\prime }}{\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right)w_{j,k^{\prime }}{\mathrm{sech}}^2\left(\sum _{i^{\prime }}^I{w}_{i^{\prime },j}{x}_{i^{\prime }}+w_{I+1,j}\right)& \text{<mi>i</mi> <mo>=</mo> <mi>I</mi> <mo>+</mo> <mn>1</mn>}\\ \sum _{l^{\prime }}^L{\beta }_{l^{\prime }}\left(y_{l^{\prime }}-T_{l^{\prime }}\right)\sum _{k^{\prime }}^K{w}_{k^{\prime },l^{\prime }}{\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k^{\prime }}{p}_{j^{\prime }}+w_{J+1,k^{\prime }}\right)w_{j,k^{\prime }}{\mathrm{sech}}^2\left(\sum _{i^{\prime }}^I{w}_{i^{\prime },j}{x}_{i^{\prime }}+w_{I+1,j}\right)x_i& \text{otherwise}\end{array}$

$\frac{\partial e}{\partial w_{j,k}}=\{\begin{array}{cc}\sum _{l^{\prime }}^L{\beta }_{l^{\prime }}\left(y_{l^{\prime }}-T_{l^{\prime }}\right)w_{k,l^{\prime }}{\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k}{p}_{j^{\prime }}+w_{J+1,k}\right)& j=J+1\\ \sum _{l^{\prime }}^L{\beta }_{l^{\prime }}\left(y_{l^{\prime }}-T_{l^{\prime }}\right)w_{k,l^{\prime }}{\mathrm{sech}}^2\left(\sum _{j^{\prime }}^J{w}_{j^{\prime },k}{p}_{j^{\prime }}+w_{J+1,k}\right)p_j& \text{otherwise}\end{array}$

$\frac{\partial e}{\partial w_{k,l}}=\{\begin{array}{cc}{\beta }_l\left(y_l-T_l\right)& k=K+1\\ {\beta }_l\left(y_l-T_l\right)q_k& \text{otherwise}\end{array}$

double Grade(std::vector<double>*, std::vector<double>*, std::vector<double>&)

This method runs the neural network using the input values passed as the first argument and then uses equation 5 given in section 3.2 to find the total error, using the second argument as the ideal output T and the third argument as the output importance $\beta$.

void Learn(std::vector<double>*, double)

This method changes the weights of the neural network. The first argument is a list of error contributions as calculated by Test. The second is a multiplying factor to apply to the error contributions. The error contributions are each multiplied by the factor and then substracted from the respective weight.

For rapid minimisation, high factors (e.g. 2) are recommended, for accurate minimisation into local minima, small factors (e.g. 0.5) are better suited.

This works by assuming that given a change in total error for a small (positive) change in a weight, the change required in the weight to minimise the error will be a proportional amount in the opposite direction. While this is a reasonable assumption given the transfer function used in this implementation, it may not be the case for other transfer functions e.g. those that are chaotic.

std::vector<double>* GetCharacteristics()

Returns a pointer to a vector containing the weights of the network, suitable for passing to the relevant constructor. The order of the values in the vector returned is internal to the FeedForwardTrilayerPerceptron implementation, as it is dependent on the exact implementation of the storage of the weights. Therefore, nothing should be assumed about the order of the values in this array.

void SetCharacteristics(std::vector<double>*)

Sets the weights of the network. The argument is a pointer to a vector containing the weights required (including those required for hidden nodes). The vector returned by GetCharacteristics() is in this format.

void RandomiseWeights(double)

Randomises the weights of the network, in the range -x..x where x is the argument.

void Save(ostream&)

Writes out the size and weights of the noural network to the stream.

The training program, after reading in a set of training and testing data sets, runs each training set through the Test() method, and updates the weights (Learn()) using the average of the resulting vectors.

During each iteration, the current set of weights is output to a file (Save()), along with the total score for that set of weights, found by adding together the result from Grade() called on each of the testing sets.

The optimal neural network (lowest score) is then used when passing the 20,000 spectra from the 2df survey through the Run() method.

3.4. Training Data

A neural network needs a large baseline to recognise patterns accurately. Unfortunately, there are only one or two known examples of typical DLAs in the 2df data. This is not enough to train a neural network. Instead, around 120 low-ionisation heavy element absorbers, DLA candidates suitable for higher resolution follow-up observations found by manual inspection of the highest S/N spectra [3], were used as positive matches. Positive matches were assigned the single ideal output 1.

For negative matches, a random cross-section of spectra was automatically selected, then screened to remove any possible DLAs in the sample (there were none). Negative matches were assigned the single ideal output -1.

The resulting set of spectra (see appendix 6) was then randomly split into a training set (80%) and a testing set (20%).

3.5. Analysis

For every combination of hidden layer sizes tried (with one unreproducible exception), the neural network, even with its optimal weights, resulted in assigning a value close to 0.7 for every spectra. This indicates that the neural network was unable to differentiate between the samples and the other 20,000 spectra.

One possible conclusion from this is that the training data did not contain patterns, or at least any patterns were too subtle.

Another possibility that might explain the lack of a successful neural network may be the presence of multiple local minima in the weight phase space. If the phase space is "rugged" in this way, the likelyhood of finding a real minimum amongst the many minor minima is based almost entirely on the starting conditions (the inital values of the weights and which data sets are used for training and which are used for testing).

This hypothesis is borne out by the one exception mentioned above. During a period of stress testing, a single run was spotted outputting different numbers. Unfortunately as this was during a test run the neural network weights were not saved.

The "rugged" phase space may be explained by the extreme variation in the input data.

3.6. Variations

The scoring algorithm was changed to sum the exponential of each testing network's error, in order to favour networks that are more accurate overall rather than those that have a few good results but mainly bad results. This was successful with test data but made little difference with the spectra data.

The network was initally run using the full 1024 data points of each spectra as the input. This was then reduced to 72 by using the high end of the fast fourier transformation. Various hidden layer sizes were also tried.

Even with hidden layers with over 100 nodes, the network still performed well, completing training and running through the 20,000 spectra in under 30 minutes.

3.7. Directions for future research

To skip around phase space without getting side tracked by local minima, the back-propagating training algorithm could be replaced by a genetic algorithm [13], using the weights as the chromosome. This would be reasonably simple to implement and should perform ever faster than the current training algorithm.

An incomplete implementation of such a system is included in CVS with the back-propagating implementation [15].

4. Appendix: References

[1] 2QZ Data Archive, 10k release B. J. Boyle, S. M. Croom, R. J. Smith, T. Shanks, L. Miller, N. Loaring, http://www.2dfquasar.org/ April 2001.

[2] Lyman alpha systems and cosmology J. D. Cohn, http://astron.berkeley.edu/~jcohn/lya.html.

[3] The 2dF QSO Redshift Survey - VIII. Absorption systems in the 10k catalogue P. J. Outram, R. J. Smith, T. Shanks, B. J. Boyle, S. M. Croom, N. S. Loaring, L. Miller, arXiv:astro-ph/0107460, 24 Jul 2001.

[4] The Anglo-Australian Telescope: A Brief History R. Bell http://www.aao.gov.au/about/aathist.html.

[5] The Anglo-Australian Telescope R. Bell http://www.aao.gov.au/about/aat.html.

[6] 2dF Home Page K. Glakebrook http://www.aao.gov.au/local/www/2df/.

[7] FITSIO W. D. Pence http://heasarc.gsfc.nasa.gov/fitsio/.

[8] The 2QZ Catalogue Format B. J. Boyle, S. M. Croom, R. J. Smith, T. Shanks, L. Miller, N. Loaring, http://www.2dfquasar.org/Spec_Cat/catalogue.html.

[9] The 2dF QSO Redshift Survey - V. The 10k catalogue R. J. Smith, T. Shanks, B. J. Boyle, S. M. Croom, N. S. Loaring, L. Miller, http://www.2dfquasar.org/Papers/2QZpaperV.ps.gz.

[10] FFTW: An Adaptive Software Architecture for the FFT M. Frigo, S. G. Johnson, 1998 ICASSP conference proceedings (vol. 3, pp. 1381-1384).

[11] Searching for Damped Lymen Alpha Systems Using an Artificial Neural Network J. S. Houghton, University of Bath, May 2002.

[12] An introduction to artificial neural networks C. A. L. Bailer-Jones, R. Gupta, H. P. Singh. MNRAS, 2001.

[13] Evolving Neural Networks D. B. Fogel, L. J. Fogel, V. W. Porto, Springer, 1990 (vol. 63, pp. 487-493). [14]

[14] Neural Network Bibliography J. Ruhland, http://liinwww.ira.uka.de/bibliography/Neural/neural.genetic.bib.gz.

[15] 2df QSO Redshift Survey Analysis: CVS I. E. Hickson, J. S. Houghton, http://sourceforge.net/cvs/?group_id=37934.

4.1. Acknowledgements

Dr. G. Mathlin and J. S. Houghton were instrumental in the completion of this project.

6. Appendix: Data Sets

The following spectra were used as positive matches.

J000259.0-312222a J000534.0-290308a J000811.6-310508a
J001123.8-292500a J001233.1-292718a J002832.4-271917a
J003142.9-292434a J003533.7-291246a J003843.9-301511a
J004406.3-302640a J005628.5-290104a J011102.0-284307a
J011720.9-295813a J012012.8-301106a J012315.6-293615a
J012526.7-313341a J013032.6-285017a J013356.8-292223a
J013659.8-294727a J014729.4-272915a J014844.9-302817a
J015550.0-283833a J015553.8-302650a J015647.9-283143a
J015929.7-310619a J021134.8-293751a J021826.9-292121a
J022215.6-273231a J022620.4-285751a J023212.9-291450a
J024824.4-310944a J025259.6-321125a J025608.9-294737a
J025919.2-321650a J030249.6-321600a J030324.3-300734a
J030647.6-302021a J030711.4-303935a J030718.5-302517a
J030944.7-285513a J031255.0-281020a J031309.2-280807a
J031426.9-301133a J095605.0-015037a J095938.2-003501a
J101230.1-010743a J101556.2-003506a J101636.2-023422a
J101742.3+013216a J102645.2-022101a J103727.9+001819a
J105304.0-020114a J105620.0-000852a J105811.9-023725a
J110603.4+002207a J110624.6-004923a J110736.6+000328a
J114101.3+000825a J115352.0-024609a J115559.7-015420a
J120455.1+002640a J120826.9-020531a J120827.0-014524a
J120836.2-020727a J120838.1-025712a J121318.9-010204a
J121957.7-012615a J122454.4-012753a J125031.6+000216a
J125359.6-003227a J125658.3-002123a J130019.9+002641a
J130433.0-013916a J130622.8-014541a J133052.4+003219a
J134448.0-005257a J134742.0-005831a J135941.1-002016a
J140224.1+003001a J140710.5-004915a J141051.2+001546a
J141357.8+004345a J142847.4-021827a J144715.4-014836a
J214726.8-291017a J214836.0-275854a J215024.0-312235a
J215034.6-280520a J215102.9-303642a J215222.9-283549a
J215342.9-301413a J215359.0-292108a J215955.4-292909a
J220003.0-320156a J220137.0-290743a J220208.5-292422a
J220214.0-293039a J220650.0-315405a J220655.3-313621a
J220738.4-291303a J221155.2-272427a J221445.9-312130a
J221546.4-273441a J222849.4-304735a J223309.9-310617a
J224009.4-311420a J225915.2-285458a J230214.7-312139a
J230829.8-285651a J230915.3-273509a J231227.4-311814a
J231412.7-283645a J231459.5-291146a J231933.2-292306a
J232023.2-301506a J232027.1-284011a J232330.4-292123a
J232700.2-302637a J232914.9-301339a J232942.3-302348a
J233940.1-312036a J234321.6-304036a J234400.8-293224a
J234402.5-303601a J234405.7-295533a J234527.5-311843a
J234550.4-313612a J234753.0-304508a J235714.9-273659a
J235722.1-303513a

The following spectra were used as negative matches.

J003910.0-285435a J005248.2-312205a J011159.9-274342a
J011512.8-301302a J012323.1-285252a J015150.9-282639a
J015656.0-282335a J022759.8-283329a J024047.4-283443a
J024231.6-285302a J024447.3-282154b J031232.7-281311b
J031353.5-274633a J031404.7-280329a J095314.4-004940a
J100528.8-012243a J101440.3+001904a J104132.3-003513a
J104536.7-023933a J104727.4+001039a J111436.3-014604a
J112009.1-005604a J112228.6-000859a J112234.9+001750a
J113153.2-011543a J115222.0+002109a J115341.1-014237a
J115518.9-010659a J115952.8-012236a J121429.5-022338a
J121456.1-012033a J122512.5-005243a J122712.7-002831a
J124831.9-001607a J131255.2-003515a J132503.6+004505a
J133727.5+003717a J134511.0-022552a J134932.9-001454a
J135123.9-004513a J135618.2-000626a J140026.5-011311a
J142533.9-014116a J144456.4-021036a J144459.2-004734a
J144717.4-012443a J214836.0-275854a J215354.9-284526a
J215420.5-275544a J220336.9-293224a J220450.9-280630a
J220707.1-282528a J224002.2-280829a J224459.7-310819a
J224830.3-310543a J225640.1-280843a J225839.6-283920b
J225900.0-272014a J225939.0-310143a J230848.0-303807a
J231212.0-283711a J231225.9-311531a J231559.2-293108a
J231748.0-302943a J231858.2-305418a J233737.9-300214a
J234446.3-275540a

7. Appendix: Source

7.1. ffmp.h

#include 
#include 

// two hidden layers
// XXX should make this a template and abstract out the use of double
class FeedForwardTrilayerPerceptron {

  public:
    FeedForwardTrilayerPerceptron(int aInputLength, int aLayer1Length,
      int aLayer2Length, int aOutputLength, double aMax);
      // initialise the weights randomly
    FeedForwardTrilayerPerceptron(int aInputLength, int aLayer1Length,
      int aLayer2Length, int aOutputLength,
      std::vector* aCharacteristics);
      // initialise the weights from a list of characteristics
    FeedForwardTrilayerPerceptron(istream& aInput);
      // initialise the weights from the stream
    virtual ~FeedForwardTrilayerPerceptron(); // forget the weights

    virtual std::vector* Run(std::vector* aInput);
     // returns the output

    virtual std::vector* Test(std::vector* aInput,
                                      std::vector* aIdealOutput,
                                      std::vector& aOutputImportance);
      // returns a list representing offsets to pass to Learn(); offsets of
      // 0 mean there's nothing to fix

    virtual double Grade(std::vector* aInput,
      std::vector* aIdealOutput,
      std::vector& aOutputImportance);

    virtual void Learn(std::vector* aOffsets, double weight);
      // uses a list of the length returned from Test() to fix the
      // perceptron's characteristics

    virtual std::vector* GetCharacteristics();
      // returns a list of characteristics
    virtual void SetCharacteristics(std::vector* aCharacteristics);

    virtual void RandomiseWeights(double max);
    virtual void Save(ostream& aOutput);

  protected:
    int Allocate(int aInputs, int aLayer1, int aLayer2, int aOutputs);
    int mInputsLength;
    int mLayer1Length;
    int mLayer2Length;
    int mOutputsLength;
    double* mWeights_ij; // input -> first layer
    double* mWeights_jk; // first layer -> second layer
    double* mWeights_kl; // second layer -> output

};]]>

7.2. ffmp.cpp

Note: Three long comments have been elided as they are more accurately represented in section 3.2.

#include "ffmp.h"

FeedForwardTrilayerPerceptron::FeedForwardTrilayerPerceptron(int aInputsLength, int aLayer1Length, int aLayer2Length, int aOutputsLength, double aMax) {
  this->Allocate(aInputsLength, aLayer1Length, aLayer2Length, aOutputsLength);
  this->RandomiseWeights(aMax);
}

FeedForwardTrilayerPerceptron::FeedForwardTrilayerPerceptron(int aInputsLength, int aLayer1Length, int aLayer2Length, int aOutputsLength, std::vector* aCharacteristics) {
  this->Allocate(aInputsLength, aLayer1Length, aLayer2Length, aOutputsLength);
  this->SetCharacteristics(aCharacteristics);
}

int FeedForwardTrilayerPerceptron::Allocate(int aInputsLength, int aLayer1Length, int aLayer2Length, int aOutputsLength) {
  // precondition: this must be called exactly once in the constructor
  mInputsLength = aInputsLength;
  mLayer1Length = aLayer1Length;
  mLayer2Length = aLayer2Length;
  mOutputsLength = aOutputsLength;
  mWeights_ij = new double[mLayer1Length*(mInputsLength+1)];
    // index in as i+j*(mInputsLength+1)
  mWeights_jk = new double[mLayer2Length*(mLayer1Length+1)];
    // index in as j+k*(mLayer1Length+1)
  mWeights_kl = new double[mOutputsLength*(mLayer2Length+1)];
    // index in as k+l*(mLayer2Length+1)
  return mLayer1Length*(mInputsLength+1) + mLayer2Length*(mLayer1Length+1) + mOutputsLength*(mLayer2Length+1);
}

#define sech(x) (1.0/cosh(x))

#define THINK                                                     \
  for (int j = 0; j < mLayer1Length; ++j) {                       \
    double p_j = 0.0;                                             \
    int jPos = j*(mInputsLength+1);                               \
    for (int i = 0; i < mInputsLength; ++i) {                     \
      p_j += mWeights_ij[i+jPos]*(*aInput)[i];                    \
    }                                                             \
    /* offset node */                                             \
    p_j += mWeights_ij[mInputsLength+jPos];                       \
    p[j] = tanh(p_j);                                             \
  }                                                               \
  for (int k = 0; k < mLayer2Length; ++k) {                       \
    double q_k = 0.0;                                             \
    int kPos = k*(mLayer1Length+1);                               \
    for (int j = 0; j < mLayer1Length; ++j) {                     \
      q_k += mWeights_jk[j+kPos]*p[j];                            \
    }                                                             \
    /* offset node */                                             \
    q_k += mWeights_jk[mLayer1Length+kPos];                       \
    q[k] = tanh(q_k);                                             \
  }                                                               \
  for (int l = 0; l < mOutputsLength; ++l) {                      \
    double output_l = 0.0;                                        \
    int lPos = l*(mLayer2Length+1);                               \
    for (int k = 0; k < mLayer2Length; ++k) {                     \
      output_l += mWeights_kl[k+lPos]*q[k];                       \
    }                                                             \
    output_l += mWeights_kl[mLayer2Length+lPos];                  \
    result->push_back(output_l);                                  \
  }                                                               \
                                                              /* end */

std::vector* FeedForwardTrilayerPerceptron::Run(std::vector* aInput) {
  assert(aInput->size() == mInputsLength);
  double* p = new double [mLayer1Length];
  double* q = new double [mLayer2Length];
  std::vector* result = new std::vector();
  THINK
  delete[] p;
  delete[] q;
  return result;
}

double FeedForwardTrilayerPerceptron::Grade(std::vector* aInput, std::vector* aIdealOutput, std::vector& aOutputImportance) {
  assert(aInput->size() == mInputsLength);
  double* p = new double [mLayer1Length];
  double* q = new double [mLayer2Length];
  std::vector* result = new std::vector();
  THINK
  double e = 0;
  for (int l = 0; l < mOutputsLength; ++l) {
    e += aOutputImportance[l] * pow((*result)[l] - (*aIdealOutput)[l], 2);
  }
  delete[] p;
  delete[] q;
  delete result;
  return e / 2.0;
}

std::vector* FeedForwardTrilayerPerceptron::Test(std::vector* aInput, std::vector* aIdealOutput, std::vector& aOutputImportance) {
  // return format from this is somewhat odd.

  // it consists of the errors in the weights in the same format as
  // the mWeights_xy memory blocks, but in the order kl, jk, ij.

  assert(aInput->size() == mInputsLength);
  double* p = new double [mLayer1Length];
  double* q = new double [mLayer2Length];
  std::vector* result = new std::vector();
  THINK

  // now work out what the error in each weight is
  std::vector* corrections = new std::vector();


  // cache some common terms
  double* lTerms = new double [mOutputsLength];

  for (int l = 0; l < mOutputsLength; ++l) {
    lTerms[l] = aOutputImportance[l] * ((*result)[l] - (*aIdealOutput)[l]);
    for (int k = 0; k < mLayer2Length; ++k) {
      corrections->push_back(lTerms[l] * q[k]);
    }
    /* offset node */
    corrections->push_back(lTerms[l]);
  }


  // cache some common terms
  double* kTerms = new double [mLayer2Length];

  for (int k = 0; k < mLayer2Length; ++k) {
    int kPos = k*(mLayer1Length+1);
    kTerms[k] = 0;
    for (int j = 0; j < mLayer1Length; ++j) {
      kTerms[k] += mWeights_jk[j+kPos] * p[j];
    }
    kTerms[k] = pow(sech(kTerms[k] + mWeights_jk[mLayer1Length+kPos]), 2);
    double value = 0;
    for (int l = 0; l < mOutputsLength; ++l) {
      value += lTerms[l] * mWeights_kl[k + l*(mLayer2Length+1)];
    }
    value *= kTerms[k];
    for (int j = 0; j < mLayer1Length; ++j) {
      corrections->push_back(value * p[j]);
    }
    corrections->push_back(value);
  }


  for (int j = 0; j < mLayer1Length; ++j) {
    int jPos = j*(mInputsLength+1);
    double jTerm = 0;
    for (int i = 0; i < mInputsLength; ++i) {
      jTerm += mWeights_ij[i+jPos] * (*aInput)[i];
    }
    jTerm = pow(sech(jTerm + mWeights_ij[mInputsLength+jPos]), 2);

    double value = 0;
    for (int l = 0; l < mOutputsLength; l++) {
      int lPos = l*(mLayer2Length+1);
      double innerValue = 0;
      for (int k = 0; k < mLayer2Length; k++) {
        innerValue += kTerms[k] * mWeights_kl[k + lPos] * mWeights_jk[j+k*(mLayer1Length+1)];
      }
      value += lTerms[l] * innerValue;
    }

    value *= jTerm;
    for (int i = 0; i < mInputsLength; ++i) {
      corrections->push_back(value * (*aInput)[i]);
    }
    corrections->push_back(value);
  }

  //for (int index = 0; index < corrections->size(); ++index) {
  //  cerr << (*corrections)[index] << " ";
  //}
  //cerr << "\n";

  delete[] lTerms;
  delete[] kTerms;
  delete[] p;
  delete[] q;
  delete result;
  return corrections;
}

void FeedForwardTrilayerPerceptron::Learn(std::vector* aOffsets, double weight) {
  // offsets are in the same format as returned from Test().
  int index = 0;
  for (int l = 0; l < mOutputsLength; ++l) {
    int lPos = l*(mLayer2Length+1);
    for (int k = 0; k <= mLayer2Length; ++k) {
      mWeights_kl[k+lPos] -= (*aOffsets)[index++] * weight;
    }
  }
  for (int k = 0; k < mLayer2Length; ++k) {
    int kPos = k*(mLayer1Length+1);
    for (int j = 0; j <= mLayer1Length; ++j) {
      mWeights_jk[j+kPos] -= (*aOffsets)[index++] * weight;
    }
  }
  for (int j = 0; j < mLayer1Length; ++j) {
    int jPos = j*(mInputsLength+1);
    for (int i = 0; i <= mInputsLength; ++i) {
      mWeights_ij[i+jPos] -= (*aOffsets)[index++] * weight;
    }
  }
}

std::vector* FeedForwardTrilayerPerceptron::GetCharacteristics() {
  std::vector* result = new std::vector();
  int index = 0;
  for (int l = 0; l < mOutputsLength; ++l) {
    int lPos = l*(mOutputsLength+1);
    for (int k = 0; k < mLayer2Length; ++k) {
      result->push_back(mWeights_kl[k+lPos]);
    }
  }
  for (int k = 0; k < mLayer2Length; ++k) {
    int kPos = k*(mLayer1Length+1);
    for (int j = 0; j < mLayer1Length; ++j) {
      result->push_back(mWeights_jk[j+kPos]);
    }
  }
  for (int j = 0; j < mLayer1Length; ++j) {
    int jPos = j*(mInputsLength+1);
    for (int i = 0; i < mInputsLength; ++i) {
      result->push_back(mWeights_ij[i+jPos]);
    }
  }
  return result;
}

void FeedForwardTrilayerPerceptron::SetCharacteristics(std::vector* aCharacteristics) {
  int index = 0;
  for (int l = 0; l < mOutputsLength; ++l) {
    int lPos = l*(mLayer2Length+1);
    for (int k = 0; k <= mLayer2Length; ++k) {
      mWeights_kl[k+lPos] = (*aCharacteristics)[index++];
    }
  }
  for (int k = 0; k < mLayer2Length; ++k) {
    int kPos = k*(mLayer1Length+1);
    for (int j = 0; j <= mLayer1Length; ++j) {
      mWeights_jk[j+kPos] = (*aCharacteristics)[index++];
    }
  }
  for (int j = 0; j < mLayer1Length; ++j) {
    int jPos = j*(mInputsLength+1);
    for (int i = 0; i <= mInputsLength; ++i) {
      mWeights_ij[i+jPos] = (*aCharacteristics)[index++];
    }
  }
}

#define RAND(max) (((max)*rand()/(RAND_MAX+1.0))-((max)/2.0))

void FeedForwardTrilayerPerceptron::RandomiseWeights(double max) {
  //cerr << "weights in range " << max << ": ";
  for (int l = 0; l < mOutputsLength; ++l) {
    int lPos = l*(mLayer2Length+1);
    for (int k = 0; k <= mLayer2Length; ++k) {
      mWeights_kl[k+lPos] = RAND(max);
      //cerr << mWeights_kl[k+lPos] << " ";
    }
  }
  for (int k = 0; k < mLayer2Length; ++k) {
    int kPos = k*(mLayer1Length+1);
    for (int j = 0; j <= mLayer1Length; ++j) {
      mWeights_jk[j+kPos] = RAND(max);
      //cerr << mWeights_jk[j+kPos] << " ";
    }
  }
  for (int j = 0; j < mLayer1Length; ++j) {
    int jPos = j*(mInputsLength+1);
    for (int i = 0; i <= mInputsLength; ++i) {
      mWeights_ij[i+jPos] = RAND(max);
      //cerr << mWeights_ij[i+jPos] << " ";
    }
  }
}

FeedForwardTrilayerPerceptron::~FeedForwardTrilayerPerceptron() {
  delete[] mWeights_ij;
  delete[] mWeights_jk;
  delete[] mWeights_kl;
}


FeedForwardTrilayerPerceptron::FeedForwardTrilayerPerceptron(istream& aInput) {
  int inputsLength, layer1Length, layer2Length, outputsLength;
  aInput >> inputsLength;
  aInput >> layer1Length;
  aInput >> layer2Length;
  aInput >> outputsLength;
  int expectedLength = this->Allocate(inputsLength, layer1Length, layer2Length, outputsLength);
  std::vector* characteristics = new std::vector();
  for (int index = 0; index < expectedLength; ++index) {
    double value;
    aInput >> value;
    characteristics->push_back(value);
  }
  this->SetCharacteristics(characteristics);
  delete characteristics;
}

void FeedForwardTrilayerPerceptron::Save(ostream& aOutput) {
  aOutput << mInputsLength << " ";
  aOutput << mLayer1Length << " ";
  aOutput << mLayer2Length << " ";
  aOutput << mOutputsLength << " ";
  std::vector* characteristics = this->GetCharacteristics();
  for (int index = 0; index < characteristics->size(); ++index) {
    aOutput << (*characteristics)[index] << " ";
  }
  delete characteristics;  
}
]]>