Introduction
Brief
Night Blindness
There has been a lot of concern recently about the vision of drivers at night. It appears that drivers with good vision, or at least vision suitably correct by spectacles, become virtually blind by night. In this Activity, you will investigate possible physical (i.e. physics) causes of night blindness.
Here are some theories:
- Less clear images are produced when light passes through larger apertures of a lens. (N.B. The pupil of the eye becomes larger as light intensity decreases).
- Lenses have different focal lengths for light of different wavelengths so the eye does not focus light from sodium street lamps in the same way as daylight.
Choose one of these theories, design and carry out an experiment to test it. N.B. The experiment must yield quantitative results.
I have opted to do the second investigation.
Plan
To find if the theory is correct, I will find the focal length of a lens using several different colours of light. To achieve the different colours, I will use the filters and lamps in the following combinations:
- White Bulb
- Sodium Lamp
- Ultraviolet Lamp
- White Bulb with Red Filter
- White Bulb with Green Filter
- White Bulb with Blue Filter
- White Bulb with Yellow Filter
- White Bulb with Cyan Filter
- White Bulb with Magenta Filter
To find the focal length of the lens at the different wavelengths, I will attempt to focus light going through a grid onto a white screen.
Method
Layout

The filter will be afixed to the grid, which acts as an object. At some distance away from the object will be the light source. The distance is required to get the rays arriving in a supposedly parallel fashion (the actual distance possible is limited since intensity decreases rather rapidly as distance increases).
On the other side of the object will be the lens, and further on still will be the screen. The image of the object, focused by the lens, will be on the screen. The whole contraption is built on a ruler, allowing the relative distances to be measured easily.
To find accurate values for the focal length, I will find the distance required (from lens to screen) to focus the grid for several different object to lens distances.
Decisions and Preliminary Investigations
Preliminary investigations with the white light showed that the focal length is in the range of 0.07 cm-1. (You can see this in the white light data, since the preliminary investigations' results were combined with the main white light results).
Preliminary work also suggested that the best range of distances (for object to lens) is 20 cm to 40 cm.
Steps
After setting up the equipment as explained above, each set of readings will progress as follows:
- Set the lens to be 20 cm from the grid.
- Move the screen from the lens away until a perfectly focused image is formed.
- Note the gird to screen distance.
- Move the screen from far from the lens inwards until a perfectly focused image is formed. It is important to complete this step as well as the second since there is always a depth of field when using a lens - a small 'tolerance' in which the image is well focused. It is not as clear cut as the term focal length would have you believe.
- Note the gird to screen distance.
- Move the screen yet again and take yet another reading of the grid to screen distance.
- Set the lens to 25 cm from the grid and repeat steps 2 to 6 again.
- Repeat step 7 with distances 30 cm, 35 cm and 40 cm.
- Change the filter and/or lamp and repeat steps 1 to 9 for this new wavelength.
- Repeat step 10 for all remaining lamp/filter combinations.
Terminology
- Object Distance
- The distance between the object (the grid) and the lens. cf: Image Distance.
- Image Distance
- The distance between the image (the screen) and the lens. cf: Object Distance.
- Focal Length
The principal focus (F) of a thin lens is the point on the principal axis towards which all paraxial rays parallel to the principal axis converge (in the case of a convex lens), or from which they appear to diverge (in the case of a concave lens), after refraction.
Since light can fall on either surface (front or back) of a lens, lenses have two principal foci, one on each side. These are equidistant from the centre (P) of the lens (provided the lens is thin and has the same medium on both sides, e.g., air).
The distance FP is the focal length of the lens.
In equations, u represents the object distance and v represents the image distance. The third variable, f, represents the focal length of the lens.
Theory
The object distance, u, the image distance, v, and the focal length, f, are related by the equation:
| 1 u |
+ | 1 v |
= | 1 f |
A quick way of measuring f is to measure the image distance required to focus a distant object. This works because if u is large, u-1 is small and so cancels.
| 1 ularge |
+ | 1 v |
= | 1 f |
becomes
| 1 v |
» | 1 f |
and this leaves
| v | » | f |
I will not be using this technique since it is not accurate enough.
The technique I will be using, which is described above, is somewhat more accurate and involves finding values of u and v, and using the equation to calculate f. There are three variations on the calculation of f by this method (the experimental steps are the same in all cases, although more data is required for the more accurate calculations).
Find one pair of values (one u and one v) and simply calculate f by using the equation
1
u+ 1
v= 1
f- The second method is to take several pairs of u and v and average the resulting fs.
The third and best method is to take even more data and to plot it. Hopefully (and theoretically) the x-axis intercept and the y-axis intercept should be equal. This is easily proved. Starting from the equation
1
u+ 1
v= 1
fwe rearrange into the y = mx + c form,
1
u= -1
v+ 1
fWhere y is equivalent to u-1, m is equivalent to -1, x is equivalent to v-1, and c is equivalent to f-1. Since the gradient, m is equal to -1, at u-1 = 0 (y = 0)
0 = -1
v+ 1
fwhich rearranges to
1
v= 1
fAnd at v-1 = 0 (x = 0)
1
u= 0 + 1
fwhich cancels down to
1
u= 1
fVery clearly then, the best fit line of the plotted data should result in a line of gradient -1 which crosses the x- and y- axes at the same point.
I have opted for the more time consuming third option.
Prediction
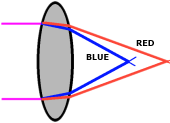
Based on research and past experience, I would suggest that the theory proposed in the brief is indeed correct. It is my belief that as the wavelength shortens (blue end), the focal length will decrease, and as the wavelength increases (red end), the focal length will get longer. This is because waves of different wavelengths are refracted by different amounts in the same material (same principle as for a prism splitting white light) and the blue light is bent more than the red light upon entering and exiting the lens.
It will be interesting to see what happens with cyan, since it's filter lets through two distinct wavelengths at opposite ends of the visible light spectrum (see results section).
Results
| Light Source or Filter | Wavelengths (nanometres) |
|---|---|
| White | 400 - 700 |
| Sodium | 589.00, 589.59 |
| Ultraviolet | 404.7 |
| Red | 700 |
| Green | 525 |
| Blue | 450 |
| Yellow | 550 - 700 |
| Cyan | 675, 400 |
| Magenta | 400 - 550 |
Forenote
All the results in the results tables and graphs are in centimetres. Technically, I should have converted my centremetre readings into metres, however, in this case it makes little difference.
Tables
There are nine tables, which give all the data (one sheet per lamp/filter combination).
Graphs
There are also twelve tables, one for each combination (all using the same scales), one for white light (to show all the data I used different scales on this graph) and two final results summary graphs (one plotting f-1, in cm-1, and one plotting f, in cm)).
Errors
| Light Source or Filter | Skew cm- 1 |
|---|---|
| White | 0.001 |
| Sodium | 0.006 |
| Ultraviolet | 0.006 |
| Red | 0.006 |
| Green | 0.006 |
| Blue | 0.006 |
| Yellow | 0.001 |
| Cyan | 0.001 |
| Magenta | 0.008 |
The data was surprisingly nice. There was one slightly abnormally high value in the blue data, a very wrong data point for the ultraviolet lamp (probably a transcript error, that is, I probably mis-noted the data during collection) and one slightly low value in the yellow data. All the other data seemed fine.
To calculate the errors, I plotted the data then drew two best fit lines: one above the data and one below. I found that actually, the gradient wasn't exactly -1. Examination of my equipment suggested that a possible reason for this is that my lens was not actually exactly above the point I was measuring each time. Indeed, I collected the data in three sets and within each set all the data has the same skew. This seems to indicate that it is experimental error.
In the case of magenta, the skew is also probably due to the large - huge - range of wavelengths involved.
What I am calling skew is the difference between the x-intercept and the y-intercept (in cm-1).
The error margins were in the order of 0.001 to 0.007 cm -1. Magenta had the biggest error range, which is to be expected since it also had the largest skew and the largest wavelength spread. White light was next, which again is normal, since it has a wavelength spread of the whole visible light spectrum.
| Light Source or Filter | ± Error cm- 1 |
|---|---|
| Magenta | 0.0071 |
| White | 0.0046 |
| Blue | 0.0024 |
| Green | 0.0021 |
| Yellow | 0.0020 |
| Sodium | 0.0019 |
| Red | 0.0016 |
| Cyan | 0.0015 |
| Ultraviolet | 0.0012 |
What is surprising is that Blue and Green light were next (note, however, that they have a much smaller error - only Magenta and White have considerable error margins). The blue error margin actually enables the "wrong" data point to be "correct" since it's error bars are within the best fit lines.
Summary
The Results Summary graphs show the trend well. They are a plot of the focal lengths of each of the filters, against the wavelengths of the filters (when I say filters, read lamps and/or filters really). There is a definite trend, as the wavelength increases, so does the focal length. Luckily for me, this is as I predicted. Three things are of note however.
- Cyan was an interesting case, I could not really understand it's pattern. This was effectively a mixture of two other filters (blue and green, theoretically) so it is not surprising that there is no obvious trend.
- Yellow was a wide band of wavelengths, but unlike Magenta (which is also a wide band) it didn't fit into the general pattern.
- Sodium seems to have "missed" the trend. This is odd as Sodium should have been a very accurate part of the experiment (it has very definite lines (it's D-lines) as it's wavelengths). I would have expected it's focal length to be about 0.1 to 0.2 cm longer.
The summary graphs do not pretend to be accurate (I have merely placed the labels on the graph, not dots) because the error bars are so relatively large that this is the only way to accurately portray the information.
Theory
The theory I put forward in the prediction matches the facts. I can therefore conclude that it is the correct one until such time as contradicting data is discovered or these results are reinterpreted.

If you recall, I suggested that the theory proposed in the brief was indeed correct. It seems that as the wavelength shortens (as in the blue end of the visible light spectrum), the focal length decreases, and as the wavelength increases (as towards the red end of the visible light spectrum), the focal length gets longer. This is probably because waves of different wavelengths are refracted by different amounts in the same material (as I said in my prediction, this is the same principle as for a prism splitting white light) and the blue light is bent more than the red light upon entering and exiting the lens.
Limitations
As always, time was an important factor limiting my work. The other factor was that the point at which something is focused is quite subjective and dependant on the user's eyesight. During the course of the experiment I asked some of my colleagues to see if they thought my screen was focused and their opinions varied.
Conclusion
The experiment would seem to indicate that Sodium lamps are not the best invention as far as good night road lighting goes, although this is not entirely true. After all, human eyes can accommodate to the required focal length as needed. We do it all the time, to look at distant objects or close ones. If one is perfectly honest, the difference in focal length is actually negligible (around half a centimetre over the whole of the visible light spectrum).
Further Research
Obviously it would be interesting to investigate the first of the two experiments suggested. It would also be interesting, in my humble opinion, to find out if there is a way of objectively ascertaining is something is focused or not. That way, the exact range could be found automatically by computer and a much more accurate study with greater emphasis on the quantitative results could be achieved.
References
- PHYSICS A Textbook for Advanced Level Students
- 2nd Edition (1987). Author: Duncan, Tom. Publishers: John Murray (Publishers) Ltd. ISBN: 0-7195-4336-3
- Philip Harris Catalogue (1)
- This resource contained the transmission charts from which I found the wavelengths for the various filters I used.
- Internet Explorer 4.01
- I used IE4 for the publishing of this document. The standards I used were HTML4 and CSS2, created by the World Wide Web Consortium.
- EMACS (text editor)
- GNU Emacs 19.34.6 (i386-*-nt4.0) of Thu Sep 25 1997 on ESME. Used for editing this document.
- Quattro Pro 6.1
- For the graphs and spreadsheet I used QPW6.