Rate of flow of fluids

Brief

The brief is as follows.

Find what effect various factors have on the rate of flow of liquid through a tube.

Preliminary Research

During preliminary research for this experiment I discovered Poiseuille's Formula,

h =	p p r4 8 V l

where p, the pressure, is described by p = hrg (more on this in the theory section), and V is the rate of flow dV / dt, thus giving

h =	p h r g r4 8 dV dt l

which rearranges to

dV dt

=

p h r g r4 8 h l

It should be noted that h, the viscosity constant, is dependant on temperature. This equation thus gives me a convienient starting point for my experimental research. I will now describe each variable and constant in the formula.

Universal Constants

p

The universal constant relating radius and circumference. 3.1415926535898 to 14 sf.

8

A scaling factor.

These two constants are the result of Stoke's Law, from which Poiseuille's formula is derived.

Slightly Less Constant Constants

r [kg m^-3]

Density of the liquid being tested. For water, this value is 1 kg m^-3

g [m s^-2]

Acceleration due to gravity. In Melksham, where this is being tested, the value is usually taken to be 9.81 ms^-2

h [N s m^-2]

The viscosity of the fluid in question. At 298K, the value for water is 0.001 N s m^-2.

Independant Variables

h [m]

The height of the liquid above the capillary tube (directly proportional to pressure in Poiseuille's equation).

r [m]

The radius of the capillary tube.

l [m]

The length of the capillary tube.

Dependant Variable

dV dt

[l s-1]

The rate of flow (this is what I will be measuring), in litres per second.

Viscosity

Viscosity is the coefficient of proportionality between the frictional force and the product of surface area × velocity gradient (at the heart of a liquid). It is generally represented by the greek letter eta, h, and has the S.I. units [N s m^-2]. Alternative units are as follows:

1. Newton seconds per meter squared (N s m^-2) - these are the Système International units.
2. Pascal seconds (Pa S) same as above, since [N m^-2] = [Pa].
3. Poiseuille (Po), equivalent to SI units
4. The Giorgi, equivalent to SI units
5. The Poise (P, equivalent to a tenth of a Giorgi).
6. Barye Seconds (old c.g.s. units)

Poiseuille

The French physician Poiseuille discovered the law discussed above in 1844 while examining the flow of blood in blood vessels. Poiseuille's Law for Fluid Flow in a Vessel assumes

1. Steady, laminar flow
2. Long rigid tube with non slip boundary flow
3. Homogenous, newtonian fluid

Method

Discussion

General Setup

The apparatus consists of a large jar with an opening at the bottom. (Constant head apparatus would have been nice but unfortunately is outside my school's budget).

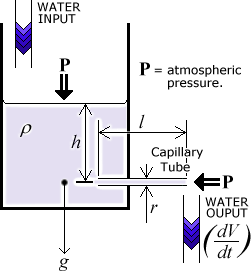
I will be placing capillary tubes of various sizes in this opening. By keeping two of my three variables constant each time, I will find the effect that (a) varying the height of the liquid (and thus the pressure, which is directly proportional to the liquid's height), (b) varying the tube length and (c) varying the tube radius, each have on the rate of flow. I am also considering changing the viscosity by using different liquids (this would also affect the density (r) and so would not immediately yield results which are "inter-liquid compatible", however one can "correct" the results by use of the formula quoted above).

Constant Height

To keep the height constant during each reading will require me to keep the input and output levels exactly equal. This is what constant head apparatus would have greatly simplified, but I will be doing this by trial and error (increase the input flow until the level of liquid is no longer decreasing, wait for the situation to stabalise, decrease the flow until the liquid level is no longer rising, repeat as required). I am expecting some small but not insignificant level of error to creep in if the height is not kept just right.

Measuring Flow

To measure the rate of flow I will collect a volume of liquid from the output tube while measuring the time it takes to flow. The actual time taken or volume collected for each reading need not be constant over the totality of my experiment since it is the rate of flow which interests me.

To collect the liquid, I will be using a measuring cylinder. Once it is filled I can place it on a flat surface such as the bench and take a reading straight off. Once that is done, I will place a themometer inside the tube and find the temperature of the liquid. I will then empty the cylinder, in preparation for the next reading. After the first time it is used, however, the cylinder will contain some droplets of the liquid, thus artificially increasing the volume measured. To prevent this slight inconsistency between the first and subsequent results I have opted to simply fill the cylinder and then empty it prior to the first reading, leaving it wet. This will cause a minute and consistent constant error.

Drying the tube between each filling is out of the question for several reasons, the first being and it is a very slow operation compared to emptying the tube (I am on quite a tight "time budget") and the second being that there is no suitable manner of doing it. A towel would get very wet very quickly, rendering it useless, and a blow dryer would increase the temperature. This is bad since it would encourage differing amounts of evaporation and may also increase the volume of the liquid (expansion by heat) although this last effect is probably so negligable as to be laughable.

I will use different sizes of measuring cylinders depending on the volume of liquid that is flowing. Whatever size I use, I will always ensure that I fill it as close as possible to the top "notch". This is to reduce the potential error. For example, with a cylinder of volume 250ml, I can measure the height to ±1ml. 1 in 250 gives a percentage error of 0.4% if I fill it to the top. However, if I only fill it with 10ml, the error is a wacking 1 in 10, in other words 10%!

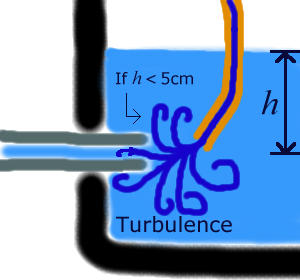
Turbulence

The lowest possible height I can measure is largely decided by what effect the liquid coming in has on the capillary tube inlet. If the liquid pouring in causes undue disturbance, then the data will be unusable. For this reason I will ensure all readings are above 5cm from the tube inlet (preliminary tests seemed to indicate this to be a reasonable height).

Sequence of Events

Before beginning, the equipment should be set up as described above. Capillary tubes should be chosen based on their lengths and radii (and eventually, a reasonable cross section of results should be found).

1. Fill the jar with the selected liquid to a low height, for example 5cm (0.05m) above the capillary tube.
2. Adjust the inflow until the liquid's level remains constant. This is a time consuming process.
3. Measure h. This is the height from the center of the capillary tube to the top of the liquid.
4. Start the timer while simultaneously placing an empty measuring cylinder under the outlet pipe, thus collecting the outflowing liquid.
5. Once enough liquid has been collected (in a 250 ml cylinder, around 240-250 ml is considered suitable) the cylinder should be removed from the flow and simultaneously the timer should be stopped.
6. The following values should be recorded:
   1. V, the volume of liquid which was collected in the measuring cylinder.
   2. t, the time it took to collect that volume.
   3. h, the height of the liquid above the middle of the capillary tube.
   4. T, the temperature of the water.
7. One can now calculate the rate of flow of water, from dividing the volume V by the time t:

   dV dt

   =

   V ÷ t

8. Each set of readings (steps iv to vii) should be taken two or (time allowing) three times. It may be necessary to fine tune the input of liquid to maintain a constant height - if one is using a tap to provide water, for example, fluctuations in the water supply can easily distrupt the level of water.
9. Once the two or three readings have been taken, the height of the water should be increased slightly (for example, by three or four centimeters), and the steps from ii to viii should be repeated.
10. Once the results for at least eight different heights have been recorded (although it may have to be less depending on the time available), the jar should be emptied (by inversion or simply by pulling the capillary tube's bung out - WARNING! This is a very wet process! Keep far away from electrical equipment!). A new capillary tube should be chosen, based on what was tested previously. At this point the entire process is to be repeated from the top.
11. Once time has run out, the final results should be tabulated, averaged, and graphed.

Theory

Pressure and Flow

Because the liquid is viscous, the pressure at the inlet of the capillary tube needs to be greater than the pressure at it's outlet for the liquid to flow. This is assuming that gravity is not affecting the flow itself - and is why I am always ensuring that the tube is horizontal. Gravity is assumed to act on the liquid in the jar itself, otherwise nothing much would happen!

The pressure at the inlet is from the weight of the liquid above the inlet, the pressure at the outlet is 0 if we ignore the atmospheric pressure.

The atmospheric pressure affects both the input of liquid and the output. First it increases the pressure (p) which is exerted on the capillary tube entrance. In fact, the actual equation of pressure would be p = hrg + P₀, where P₀ is the atmospheric pressure. Secondly, the atmospheric pressure would impose itself on the output side of the capillary tube, reducing the actual flow. Since these two amounts cancel themselves exactly (P₀-P₀ = 0) I am justified in ignoring atmospheric pressure.

Mathematical proof

Pressure at the inlet:

p_inlet = h r g + P₀

Pressure at the outlet:

p_outlet = P₀

Pressure on the liquid, inducing flow:

ptotal	= pinlet - poutlet
	= hrg + P0 - P0
	= hrg

Thus atmospheric pressure can be ignored.

Sources of Error

If we are to assume that Poiseuille's Equation is valid, which is likely since I found it quoted in several text books, then it can be predicted that changes in radius will have the biggest effect on flow. This is because it is raised to the fourth power in the equation. This also means that minute errors in the measuring of the radius will have a huge effect on the accuracy of the data. For this reason it was decided to use an accurate Vernier Caliber to find the capillary tube radii.

Predictions

My prediction is quite simply that rate of flow is modelled accurately by Poiseuille's Equation. During my research, however, I discovered that it only applies when the flow is not turbulent. One thing I am going to hopefully discover is what causes turbulent flow. I already know, from research and common sense, that if the pipe pouring liquid in, keeping the level constant, is too close to the capillary tube inlet then turbulence will cause a breakdown in the following of Poiseuille's Equation.

Summary of predictions

Height:

dV dt

µ

h

Length:

dV dt

µ

1 l

Radius:

dV dt

µ

r4

Plus, provided I get to change the liquid,

Density:

dV dt

µ

r

Viscosity:

dV dt

µ

1 h

Changes and Decisions

Multiple Liquids

It would have been nice to test multiple liquids, however only water was easily available. Various other liquids were considered (including various oils and alcohols) but were not available in the required quantities. Another problem was how to circulate the liquid so that we did not waste any (liquids other than water tend to be quite expensive!).

It was thus decided to forego the multiple-liquid idea and concentrate on water.

The short tube

We started to take readings for a very short (0.055m) tube, but we quickly abandoned the idea. The reason for this is that the glass was broken and we considered the probable magnitude of error involved was not worth it. Furthermore, the end of the rube was very sharp, posing a possible health hazard.

Results

The results have been included seperately.

Validity of the Results

Temperature

The temperature varied by ±7K, which originally concerned me since I knew that viscosity is dependant on temperature. This meant that many of my results were not usable! One possible way around this was to find the viscosity of water at each temperature and then adjust my data as dictated by Poiseuille's equation. However, after doing further research I found that h doesn't vary range for water - at least not over such a small temperature range (as it does for some other liquids, eg, oil). This means that my data is comparable without adjustment.

All but one of the tubes used classified as fast flowing, and so I used a 250ml measuring cylinder for these. For the very narrow tube I used a 10ml measuring cylinder. This affects the error considerations, as mentioned below.

Error Considerations

Radius

The error in measuring the radius was low, due to the use of a Vernier Caliber. The error d r in measuring the diameter is ±0.00005m, a half of a tenth of a millimeter (half of the graduation mark seperation). Note that the radius for the "tiny bore tube" is considerably smaller than we could measure with the Vernier Caliber - the value we have was printed on the label attached to the tube. No error information was included.

The radius is raised to the fourth power in the only graph which uses it, however, which increases the error on the graph four fold, making it ±0.00005m × 4 = ±0.0002m. This makes the data I have collected absurdly insignificant (see the graph to see why: the error bars are larger than the axes!).

The percentage error for each data point is worked out from the following equation:

dr4 r4

=

4 ×

dr r

Length

The error in measuring the length is similar in concept to that of the radius. The measurment tool was a meter ruler, error (d l) ± 0.0005m (half of the graduation mark seperation).

Since nothing special is done to the length, the percentage error is very simply

dl l

and the magnitude is 0.0005m.

Height

The error in measuring the height is identical to that of the length since the measurment tool was the same. Error (d h) is therefore ± 0.0005m (half of the graduation mark seperation), percentage error is therefore

dh h

Rate of Flow

Here we finally have an interesting variable, needing some careful consideration.

The error in the rate of flow comes from the error (d V) in the measuring of the volume which flowed, and the error (d t) in the timing of the time it takes to flow.

The error in the time taken is 0.5s (actually, the error is about 0.4s, but due to the innacuracies of using milliseconds when the timing is being done by hand I decided to only record the time data to the nearest second, thus mathematically the error is 0.5s).

The error in the volume is slightly more complicated, since it depends on which results you are discussing. For the the 0.000325m tube, we used a 10ml cylinder, since flow was so slow. For this, the error (d V_10ml) is 0.0002l, (again, this is half of the graduation mark seperation). For the other tubes, we used a 250ml cylinder (flow was appreciably faster). This tube has a greater error (d V_250ml) of 0.001l.

The percentage error of the rate of flow is therefore:

d dV dt dV dt

=

dV V

+

dt t

Which leads to...

d dV dt

=

dV dt

×

(

dV V

+

dt t

)

Temperature

The error in measuring the temperature is that of the accuracy of the measurment tool, the themometer. That was (d T) ± 0.5K (half of the graduation mark seperation). The percentage error is therefore

dT T

Analysis

Effect of Height (pressure)

General Analysis

Each height/flow graph had the same pattern: a basically straight line which gradually curves as height increases. The straight line section is a pure demonstration of Poiseuille's Equation, which states that flow is directly proportional to height. This is what I predicted.

dV dt

µ

h

However, I had not predicted the curve.

Poiseuille's equation only applies to liquid flow at low pressure, in relatively short tubes with relatively narrow radii. This is because it applies to perfect flow, not turbulent flow. At higher pressures, longer lengths or with wider bores, turbulence sets in, along with it's associated chaos.

I have come to believe that the curve is due to turbulence slowing/hindering the flow.

Constant Error

On the 0.0033m radius graph, two of the lines cross 0.005 l s^-1 and the other crosses 0.010m l s^-1. The other two graphs (both of smaller radii) both went through the origin. My guess is that for the wider bore, the water may have been pulled out by gravity since the radius was significant and so flow was not only affected by pressure.

Odd data

Radius 0.0033m

One data point in particular sticks out as irregular, on the 0.947m length line at a height of 0.2m - this is probably due to human error. Two others are slightly lower than expected, those on the 0.31m length line at heights of 0.075m and 0.016m. Since all three of the data points are lower than they "should" be, it may be that during the sampling of the out-flowing liquid we spilled a little.

Radius 0.00195m

The data points seem reasonable, the best fit line lies comfortably within the error bars.

Radius 0.000325m

This graph sports too little data to indicate any possible oddities.

Effect of Length

General Analysis

Unfortunately, there were only a limited number of tubes, which meant that we could not vary the length much without changing the radius too (we did not want to change the radius when comparing lengths since one cannot plot a graph of data where more than one variable has been changed and expect to gain a valid insight into the physics of the situation, because the other factors changed will also affect the results being compared and it is generally impossible to say what is affecting what). We did find three tubes of varying lengths and equal radius, though. The radius in question was 0.0033m.

So while the Tube Length against Rate of Flow graph does not have enough data point to allow a numerical analysis, it does let us have a fair guess as to what effect the increasing the length is. And as my physics teacher Mrs Turner told me, physics is all about guessing. It would seem that as length increases, the rate of flow decreases.

Although it is as I predicted, and as is found by Poiseuille during his research, the effect of length on flow is one which I cannot completely explain. It seems counter intuitive - when one first thinks about it, length shouldn't have any effect. It is probably due to increased friction with the capillary tube side.

It should be noted that the relationship did seem remarkably non-linear. This may have been caused by irregularities on the inside surface of one of the three pipes - to be fair and correct, we should have used several pipes of identical dimensions, averaging similar results and casting aside any odd data points, to be examined or re-measured later. This was not possible since only one pipe of each dimension was made available to us and we did not have unlimited time.

The accentuated curve could have been caused by turbulence, of course. After a great length, in addition to the effect of friction, the water stream lines probably "folds" on themselves. This would dramatically slow the flow.

Odd data

There was not enough data to identify any single invalid data points. As mentioned above, it is quite possible that one of the three sets was completely invalid.

Effect of Radius

General Analysis

The situation with the Effect of Radius Changes on Rate of Flow are even more difficult than with effect of length on rate of flow, since I have even less data to compare.

However, I will not let such a minor point hinder my efforts. The graph would seem to indicate that the bigger the bore of the capillary tube, the faster the water flowed. By saying this, however, I am putting myself at risk of being caught by the "State the Obvious Police".

What is slightly less obvious (to the uninitiated) is that the data does seem to follow a roughly y=x⁴ or (within the error bars) y=x⁵ relationship, if we assume that all three data points are near perfect. This (y=x⁴) is agreed by Poiseuille's equation (and thus by my prediction). It should be emphasised though that the above mentioned assumption is not a valid one, with only three readings one cannot make valid mathematical extrapolations.

Again... the curve may have been caused by the ever present turbulence. Poiseuille's equation does come with the disclaimer that it applies especially to narrow bores, and the curve seems to occur especially once the radius is large. This is difficult to tell exactly with only three points, though.

Odd data

There was not enough data to identify any single invalid data points. The data was not quite as expected however - the straight line was a bit too curved!

Note on Temperature Graph

As noted on this graph, the experiment was undertaken in two different rooms. The water in room 14 was distinctly warmer than in room 15. The percentages show the percentage of readings taken at the particular water temperature. As discussed in the errors section, the range of temperatures was insignificant.

Turbulence

Having been intrigued by the fact that turbulence seemed to frequently rear it's ugly head, and having been unable to formulate a mathematical model for the situation, I returned to my research and found that turbulence is still a field in which scientists are looking for solutions.

Some theories I came across suggested that a new Universal Constant may be involved, some that this was a demonstration of chaos theory, and others that it was the result quantum effects.

What is known is that turbulence can in general be ignored if the readings are taken over a long enough time - this would seem to indicate that I should have collected a great deal more water for each reading. The turbulence acts on the capillary tube's surface.

It would seem that the jury is still out on this one.

Calculating Viscosity

When I used Poiseuille's Equation (given in the introduction) to work out the viscosity of water according to my data, I calculated 3.604×10^-6 N s m^-2 ± -0.421×10^-6. This is far outside (including the error range) of the "official" figure of 1×10³ N s m^-2. The reason for this is probably that either (a) my error estimates are way to optimistic (i.e. the error was bigger due to human failings) or (b) the data itself if somehow terribly flawed by some constant error. (The data generally agreed with itself, so it was not the typical wildly out reading sending the averages to New Zealand).

Calculation

The number was found by calculating the viscosity as predicted by each set of averaged readings, of which there are 35, and averaging them. The error was calculated by doing the same again, but using the minimum and maximum values which I calculated when doing the error bars.

Limitations

In addition to the basic errors mentioned in the Errors section, which are due to equipment limits, we had some other limitations and problems reducing the accuracy of our data.

The first is pure human error. Since this experiment was not performed using automatic (electronic) recording equipment, human error is quite significant and can account for most of the oddities in the results. Unscheduled translational motion (accidental knocks), optical misalignment (reading the wrong value) or even forgetting something are all potential sources of error.

Furthermore, the equipment may not have been as perfect as we could have hoped for. Rough surfaces in the tubes, badly printed meter rulers, mis-calibrated Vernier calibers, and thermometers with air bubbles in them are all examples of this. External sources, such as fluctuations in the water supply, may also have been present (in fact, a fluctuating water supply is a certainty, since steady flow sometimes suddenly became rapidly rising currents without any intervention on our part!).

Surface tension and capillary attraction would both have been active during this experiment too, although I did not take these into consideration at any point. Capillary action would be (especially in narrow tubes) pulling the water out of the pipes faster than the pressure itself would. Surface tension would hold the water back at lower water heights, preventing any water from flowing without a minimum initial pressure.

One final limitiation we were aware of is that during the course of the experiment a cockroach was swimming on the surface of our water. While this should not have had any pronounced effect, if it was a clever and mean cockroach it may have blocked the entrance of the capillary tubes when we were not looking! I am assuming it was a dead cockroach.

Conclusion

Many factors affect the flow of liquids. While this experiment was limited by time, it showed the in general Poiseuille did a good job, but that he did not take any account of turbulence. There is a great deal more research which could be done, including using other liquids, different temperatures and trying to completely explain turbulence.

Bibliography Acknowledgements and Resources

PHYSICS A Textbook for Advanced Level Students

2nd Edition (1987). Author: Duncan, Tom. Publishers: John Murray (Publishers) Ltd. ISBN: 0-7195-4336-3

DejaNews

http://www.dejanews.com/

Infoseek Ultraseek

http://www.infoseek.com/

Usenetters

In particular Éric Lewin and Bruno Thièle, who were discussing the units of viscosity.

Internet Explorer 4.01

I used IE4 for the publishing of this document. Authoring was done using a program I wrote myself (using Delphi), available at http://www.bath.ac.uk/%7Epy8ieh/programs/htmlwriter.html. The standards I used were HTML4 and CSS2, created by the World Wide Web Consortium.

Quattro Pro 6.1

For the graphs and spreadsheet I used QPW6, which I would still recommend although during the course of this project it did lose 5 hours of my work!

I did not usse a spel chekerr.